La elipse

La elipse es una curva cerrada y plana, que se define como el lugar geométrico de los puntos del plano cuya suma de distancias r+r’, a dos puntos fijos F y F’, denominados focos, es constante e igual a 2a, siendo 2a la longitud del eje mayor A-B de la elipse.

La elipse tiene dos eje, el eje mayor A-B, también llamado real, y el eje menor C-D, ambos se cruzan perpendicularmente en el centro O de la elipse.

La longitud del eje mayor es 2a, la del eje menor 2b y la distancia focal 2c, y se cumple que a² = b² + c².

La elipse es simétrica respecto a los dos ejes.

Las rectas que unen un punto cualquiera de la elipse P, con los focos, se denominan radios vectores r y r’, y por definición se cumple que r + r’ = 2a.

Propiedades y elementos

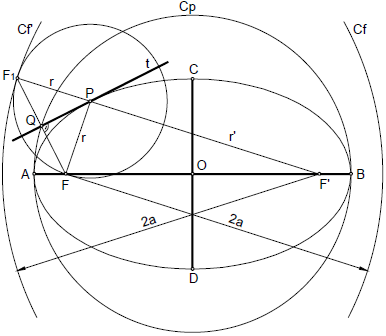
Se denomina circunferencia principal Cp, a la circunferencia de centro O, y diámetro 2a. La circunferencia principal, se define como el lugar geométrico de los pies de las perpendiculares(Q), trazadas desde los focos a las tangentes (t) de la elipse. También se puede definir como el punto medio de los segmentos que unen un foco, con la circunferencia focal del otro foco, y las mediatrices de dichos segmentos, son tangentes a la elipse

Se denomina circunferencia focal Cf, a la circunferencia de centro en uno de los focos de la elipse, y radio 2a. En una elipse se podrán trazar dos circunferencias focales. La circunferencia focal, se define como el lugar geométrico de los puntos simétricos del otro foco (F1), respecto a las tangentes (t) de la elipse.

Observando la figura, también podemos definir la elipse, como el lugar geométrico de los centros de circunferencia que pasan por un foco, y son tangentes a la circunferencia focal del otro foco.

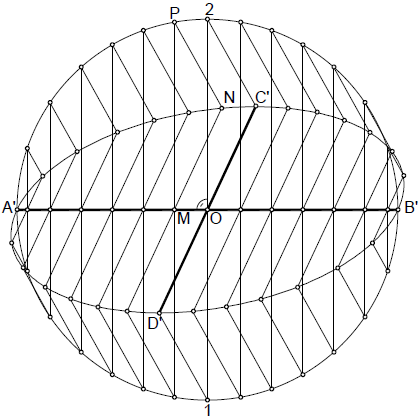
Concepto de diámetros conjugados

Si tenemos un diámetro de la elipse A’B’, el diámetro conjugado con él, es el lugar geométrico de los centros de las cuerdas paralelas a dicho diámetro (1, 2, 3, 4, etc.), estos centros determinan el diámetro conjugado D’C’ del dado.

Los ejes reales de la elipse, son los únicos diámetros conjugados perpendiculares entre si.

Mediante dos diámetros conjugados, podremos construir la elipse directamente, o bien obtener los ejes reales de la misma.

Obtención de los ejes reales, a partir de dos ejes conjugados

Dados los ejes conjugados de una elipse A’B’ y C’D’, podremos obtener a partir de ellos los ejes reales de la elipse, para ello seguiremos los siguientes pasos:

1.- Por O, centro de la elipse, trazaremos la perpendicular al eje conjugado A’B’, y sobre el llevaremos la distancia O-A’, determinando el punto 1.
2.- Uniremos el punto 1 con C’, y determinaremos el punto medio 2, de dicho segmento.
3.- Con centro en 2, trazaremos un arco de radio 2-O, que determinará sobre la prolongación del segmento 1-C’, los puntos 3 y 4. Las rectas O-3 y O-4 determinan las direcciones perpendiculares de los ejes reales de la elipse.
4.- Con centro en 2 trazaremos la circunferencia de diámetro 1-C’. Uniendo el centro O con 2, determinaremos sobre dicha circunferencia, los puntos 5 y 6, siendo las distancias O-5 y O-6, las dimensiones de los semiejes reales de la elipse.
5.- Solo resta llevar, mediante los correspondientes arcos de circunferencias, las dimensiones anteriores sobre las direcciones de los ejes, obteniendo así los ejes reales de la elipse AB y CD.

Trazado de la elipse mediante radios vectores

Teniendo en cuenta la definición de la elipse, como el lugar geométrico de los puntos del plano, cuya suma de distancias a los focos es igual a 2a, longitud del eje mayor de la elipse, solo necesitaremos coger pares de radios vectores, cuya suma sea 2a, para ello determinaremos una serie de puntos sobre el eje mayor 1, 2, 3etc., y cogeremos como parejas de radios vectores, los segmentos A1-B1, A2-B2, A3-B3, y así sucesivamente, determinando los puntos 1′, 2′, 3′, etc. de la elipse.

Con cada pareja de radios vectores, se determinarán cuatro puntos de la elipse, uno en cada cuadrante de la misma.

Cuanto mayor sea el número de puntos, mayor será la precisión del trazado de la elipse, que deberá realizarse, o bien a mano alzada o mediante reglas flexibles, o plantillas de curvas especiales.

Trazado de la elipse por haces proyectivos

Trazaremos el rectángulo AOCE, y dividiremos los lados AO y AE en un mismo número de partes iguales.

Seguidamente iremos trazando las rectas C1-D1, C2-D2, etc. y en sus intersecciones iremos obteniendo puntos de la elipse. Esto se repetirá para los cuatro cuadrantes de la elipse.

Trazado de la elipse por haces proyectivos, dados dos ejes conjugados

Trazaremos el romboide A’O’C’E’, y dividiremos los lados A’O’ y A’E’ en un mismo número de partes iguales.

Seguidamente iremos trazando las rectas C’1-D’1, C’2-D’2, etc. y en sus intersecciones iremos obteniendo puntos de la elipse. Esto se repetirá para los cuatro cuadrantes de la elipse.

Trazado de la elipse por envolventes

Esta construcción se basa en el hecho de que la circunferencia principal de una elipse, es el lugar geométrico de los pies de las perpendiculares trazadas desde los focos a las tangentes a la elipse.

Para este trazado partiremos de puntos de la circunferencia principal, como el P, indicado en la figura. Uniremos dicho punto con el foco F, y trazaremos por P la perpendicular al segmento PF, obteniendo la recta t, tangente a la elipse. Repitiendo esta operación, obtendremos una serie de tangentes que irán envolviendo a la elipse.

Trazado de la elipse a partir de circunferencias afines

Comenzaremos trazando las circunferencias de centro O, y diámetros AB y CD.

Seguidamente trazaremos radios como el O1, que corta a las circunferencias anteriores en los puntos 1 y 2. Por dichos puntos trazaremos las paralelas a CD y ABrespectivamente. Dichas paralelas se cortan en el punto 3, que es de la elipse. El número de radios trazados, serán los necesarios para definir suficientemente la elipse.

Trazado de la elipse a partir de dos diámetros conjugados por triángulos semejantes afines

Partiendo de los ejes conjugados A’B’ y C’D’, comenzaremos trazando la circunferencia de centro O y diámetro A’B’.

Sobre la circunferencia anterior, trazaremos cuerdas perpendiculares a A’B’, como la 1-2. Uniendo 2 con C’, y 1 con D’, obtendremos los triángulos O2C‘ y O1D’. Solo restará construir en el resto de cuerdas triángulos semejantes a estos como el MPN, de lados paralelos al triángulo O2C’, obteniendo así puntos de la elipse.